更新了之后,图片显示不全了
回复内容
BODY
{
FONT-FAMILY: NYT Imperial + Noto Sans SC;
FONT-SIZE: 18pt;
LINE-HEIGHT : 2.0em;
overflow: scroll;
height: 100%;
}
html {
height: 100%;
width: 100%;
overflow: hidden;
}
table {
margin: 0.5rem 0.5rem 0.5rem 0rem;
border-collapse: collapse;
font-size: 14pt;
FONT-FAMILY: Times Ten LT Std Roman;
FONT-SIZE: 16pt;
LINE-HEIGHT : 2.0em;
}
table th {
background:#5A97D5;
color: white;
width: auto;
FONT-FAMILY: Times Ten LT Std Roman;
FONT-SIZE: 16pt;
LINE-HEIGHT : 2.0em;
}
td {
width: auto;
border: 1px solid;
border-color:black;
padding:0 0.5em;
}
BODY1
{
COLOR: white;
BACKGROUND-COLOR: #000080;
}
a:link {color:#000099}
a:visited {color:#000066}
a:hover {color:#6600CC}
a:active {color:#3333FF}
ul {
list-style-type:decimal;
border-left:2pt solid #e5e5e4;
position:relative;
padding-left:35pt;
padding-top:0pt;
margin-top:5pt;
margin-bottom:5pt;
margin-left:2.5pt;
LINE-HEIGHT : 2.5em;
margin:10px;
}
ol {
list-style-type:decimal;
border-left:2pt solid #e5e5e4;
position:relative;
padding-left:35pt;
padding-top:0pt;
margin-top:5pt;
margin-bottom:5pt;
margin-left:2.5pt;
LINE-HEIGHT : 2.5em;
margin:10px;
}
.ScrollingHint{
BACKGROUND-COLOR:blue;
COLOR: white;
FONT-SIZE:14pt;
float:right;
border-bottom:5px solid #dbdbdb;
left: 5px;
top: 5px;
}
HR {
color:#F0F0F0;
TEXT-INDENT : 0em;
}
qvq {
border-bottom:thick dotted #ff0000;
border-bottom-width:1px;
}
.instantpaste1 {
border-bottom:thick dotted #ff0000;
border-bottom-width:1px;
}
.Fuck_Lexicon {
position:absolute;
top:-9999px;
left:-9999px;
color:white;
}
.jigsawlatex {
LINE-HEIGHT:2em;
}
h1 {
padding:5px 0;
font-weight:800;
border-bottom:1px solid #dbdbdb;
}
h2 {
padding:5px 0;
font-weight:800;
border-bottom:1px solid #dbdbdb;
}
h3 {
padding:5px 0;
font-weight:800;
border-bottom:1px solid #dbdbdb;
}
h4 {
padding:5px 0;
font-weight:800;
border-bottom:1px solid #dbdbdb;
}
h5 {
padding:5px 0;
font-weight:800;
border-bottom:1px solid #dbdbdb;
border-right:0px;
}
h6 {
padding:5px 0;
font-weight:800;
border-bottom:1px solid #dbdbdb;
border-right:0px;
}
.Cloze {
BACKGROUND-COLOR:#FFFF00;
COLOR:red;
FONT-STYLE:normal;
FONT-WEIGHT:bold;
FONT-SIZE:21pt;
margin:4px;
}
.clozed {
BACKGROUND-COLOR:#E9C3B9;
}
.Extract {
BACKGROUND-COLOR: #CDEDF6;
}
.headers {
BACKGROUND-COLOR: #C6C6FF;
COLOR: #000000;
FONT-WEIGHT: bold;
}
.RefText {
BACKGROUND-COLOR: #FFFFC4;
COLOR: #000000;
FONT-WEIGHT: bold;
}
.Reference {
background:linear-gradient(135deg,#57ca85 0%,#184e68 100%);
border-radius:5px;
color:#C1C1C1;
FONT-SIZE:12pt;
}
.Highlight {
BACKGROUND-COLOR:#FFFF86;
COLOR:#FF0000;
FONT-WEIGHT:bold;
}
.SearchHighlight {
BACKGROUND-COLOR:#EE8888;
COLOR:#191919;
FONT-STYLE:normal;
FONT-WEIGHT:bold;
}
.SearchHighlight1 {
BACKGROUND-COLOR:aqua;
COLOR:black;
FONT-STYLE:normal;
FONT-WEIGHT:bold;
}
.Ignore {
BACKGROUND-COLOR:#FFFF86;
COLOR:#191919;
FONT-STYLE:normal;
FONT-WEIGHT:bold;
}
table {
margin:4rem auto;
}
.TableLabel {
BACKGROUND-COLOR:#CCCCCC;
COLOR:blue;
}
.hint {
BACKGROUND-COLOR:#E0E0E0;
}
.note {
FONT-SIZE:smaller;
}
.term {
background-color:#faeecf;
padding-right:0.3em;
}
.hashtag {
border-radius:15px;
background-color:#C0D9D9;
padding-right:0.3em;
FONT-SIZE:12pt;
FONT-STYLE:italic;
}
.english_tag {
border-radius:15px;
background-color:#C0D9D9;
padding-right:0.3em;
FONT-SIZE:11pt;
FONT-STYLE:italic;
}
div.mytag {
BACKGROUND-COLOR:#DAB6B6;
COLOR:#000000;
FONT-STYLE:italic;
FONT-WEIGHT:normal;
FONT-SIZE:9.3333333333pt;
float:right;
padding:0 .3em 0 .3em;
margin-right:.3em;
border-bottom:3px solid #dbdbdb;
}
.grey {
BACKGROUND-COLOR:#DAB6B6;
COLOR:#000000;
FONT-STYLE:italic;
FONT-WEIGHT:normal;
FONT-SIZE:12pt;
}
.schedule {
border-radius:15px;
background-color:#C0D9D9;
padding-right:0.3em;
FONT-SIZE:14pt;
}
$$
\begin{aligned}
\lim _{x \rightarrow 0} f^{\prime}(x) &=\lim _{x \rightarrow 0} \frac{\left[g^{\prime}(x)+\mathrm{e}^{-x}\right] x-\left[g(x)-\mathrm{e}^{-x}\right]}{x^{2}} \\
&=\lim _{x \rightarrow 0} \frac{g^{\prime}(x)+\mathrm{e}^{-x}}{x}-\lim _{x \rightarrow 0} \frac{g(x)-\mathrm{e}^{-x}}{x^{2}} \\
& \stackrel{L^{\prime}}{ } \lim _{x \rightarrow 0}\left[g^{\prime \prime}(x)-\mathrm{e}^{-x}\right]-\lim _{x \rightarrow 0} \frac{g^{\prime}(x)+\mathrm{e}^{-x}}{2 x} \\
&=g^{\prime \prime}(0)-1-\frac{1}{2}\left[g^{\prime \prime}(0)-1\right] \\
&=\frac{1}{2}\left[g^{\prime \prime}(0)-1\right]=f^{\prime}(0),
\end{aligned}
$$
故 $f^{\prime}(x)$ 在 $(-\infty,+\infty)$ 上连续.


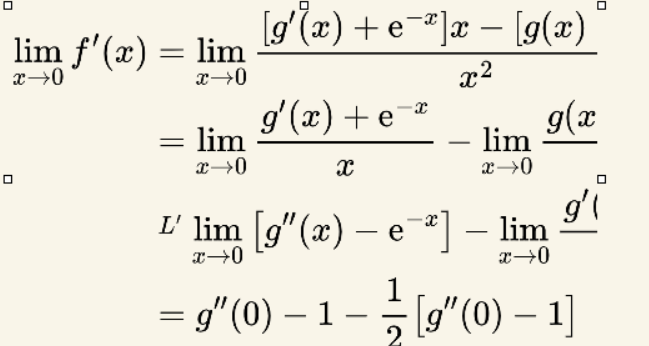
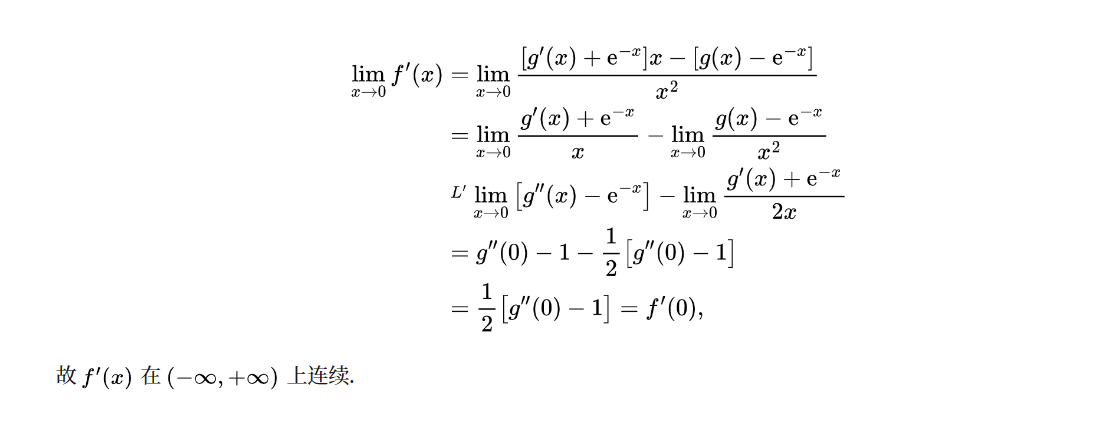

 京公网安备 11010502053266号
京公网安备 11010502053266号